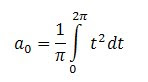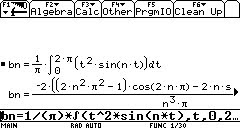SERIES DE FOURIER
DEFINICIÓN.
La serie de funciones de la forma
o , de modo mas conciso, la serie de forma
o , de modo mas conciso, la serie de forma
se llama serie trigonométrica. Los números constantes a0, an y bn (n = 1, 2, . . .) se llaman coeficientes de la serie trigonométrica
Si la serie converge, su suma es una función periódica f(x) de período 2p, puesto que sen nx y cos nx son funciones períodicas de período 2p.
De este modo,
f(t) = f (t+2p)
Si la serie converge, su suma es una función periódica f(x) de período 2p, puesto que sen nx y cos nx son funciones períodicas de período 2p.
De este modo,
f(t) = f (t+2p)
Coeficientes de Fourier de la función f(t)
Frecuencia Angular
Por Edwin Chiluisa
Ejemplo de funciones en Series de Fourier
Para entender mejor lo que es una serie de fourier es mejor realizar un ejemplo.
Descomponer en serie de Fourier la función analítica f(t) = t2 de período 2p, dibujar la gráfica de la función para -6p t 6p
Se grafica primero la función f(t)
Calculamos los coeficientes de fourier
y expresando en Serie de Fourier, queda
Por Carolina Ríos.
Calculamos los coeficientes de fourier
y expresando en Serie de Fourier, queda
Por Carolina Ríos.
Una manera más rápida y fácil de resolver el ejemplo anterior, es utilizando una calculadora (voyage 200), tal como se indica:
Por Andrés Cáceres
Si no tenemos al alcance una buena calculadora, una forma sencilla para calcular los coeficientes de Fourier del ejercicio es usando fórmulas básicas de integrales, tal como se muestra a continuación.
Tenemos que:
Por Danny Valencia
Utilizando una calculadora, también se puede graficar la serie de Fourier con su respectiva respuesta tal como se indica:
Por Jaime Vela
